Depuis toujours, il nous paraît intuitivement aller de soi qu’il n’y a qu’un temps qui baigne l’Univers et que les notions d’antériorité, de simultanéité et de postériorité sont valables partout. Ainsi on peut imaginer ce qui se passe très exactement maintenant sur une planète d’une étoile de la galaxie d’Andromède. Pourtant, au début du XX° siècle, Einstein va nous montrer que le temps dépend du référentiel dans lequel on le mesure, qu’il n’est donc pas le même partout, pire, que la notion de simultanéité n’a rien d’intangible ; en un mot, que le temps est relatif.

La relativité selon Giordano Bruno et Galilée

On savait depuis Giordano Bruno [1] et surtout depuis Galilée [2] que la vitesse était un concept relatif. Cela signifie qu’une vitesse n’a de sens que si on précise par rapport à quoi on la mesure, ce qu’on appelle le référentiel. Empressons-nous d’ajouter que ceci s’applique à la vitesse mais non pas à l’accélération : l’accélération est un concept absolu qui ne dépend pas du référentiel dans lequel on la mesure, il suffit de ressentir à l’intérieur d’un véhicule l’effet d’un coup de frein pour s’en persuader ! Mais revenons à la vitesse. Si on considère deux fusées identiques qui se déplacent l’une vers l’autre suivant un mouvement rectiligne uniforme, c’est-à-dire en ligne droite et à vitesse constante, on peut choisir une infinité de référentiels, tous aussi valides les uns que les autres, pour mesurer leurs vitesses. Par exemple, on peut se placer au centre de gravité des deux fusées et considérer qu’elles se déplacent toutes deux dans notre direction avec la même vitesse v. Mais on peut également se placer dans la première fusée, que l’on va donc considérer immobile, et mesurer que la seconde se déplace vers nous avec la vitesse 2v. De même, on peut choisir le référentiel de cette dernière fusée : cette fois ce sera cette fusée qui sera immobile tandis que la première fusée se déplacera à la vitesse 2v en sens inverse. Et ces trois points de vue ont raison, il n’y en a aucun qui est plus valide que les autres. Ceci implique que la notion de vitesse nulle, c’est-à-dire de repos absolu, est elle aussi relative : on peut toujours prendre comme référentiel un point qui n’est soumis à aucune accélération. C’est ce qu’on appelle un référentiel galiléen. Ainsi, par exemple, si vous êtes dans un train qui se déplace à vitesse constante sur les rails, vous avez tout-à-fait le droit de considérer que vous êtes au repos et que ce sont les rails, les gares, le paysage qui se déplacent par rapport à vous. Aucune expérience quelle qu’elle soit, de physique ou autre, ne viendra contredire le fait que vous êtes au repos. Contrairement au coup de frein de tout à l’heure, si vous êtes dans un wagon sans fenêtre, rien ne vous permettra de dire si ce wagon est immobile ou se déplace avec une vitesse constante par rapport aux rails. Ce principe physique, appelé relativité galiléenne ou relativité de l’espace, a fini par s’imposer à tous les scientifiques au cours du XVII° siècle.

La vitesse de la lumière est une constante

Vers 1865, Maxwell réalise la synthèse de toutes les études que ses prédécesseurs ont menées concernant l’électricité et le magnétisme [3]. Ces travaux seront finalement résumés par quatre équations [4] qui, montrant que l’électricité est indissociable du magnétisme, englobent ce qu’on appelle maintenant l’électromagnétisme et, au-delà, contiennent toute l’optique, les ondes radios, les rayons X, etc. L’apport de Maxwell à l’électromagnétisme est complètement équivalent à l’apport de Newton pour la mécanique, c’est-à-dire la synthèse géniale de tous les travaux précédents dans un même cadre unificateur. Et l’enthousiasme des physiciens de cette époque est tel qu’on croit voir arriver la fin de la physique théorique, tous ses domaines ayant été brillamment résolus. Seulement, un problème apparemment infime apparaît : dans les équations de Maxwell se trouve une constante, c, qui n’est autre que la vitesse de la lumière. Mais comment une vitesse, c’est-à-dire une grandeur relative, qui dépend du référentiel dans lequel on la mesure, peut-elle être une constante, donc absolue ? La volonté de répondre à cette question va animer les physiciens théoriciens pendant toute la fin du XIXe siècle et les premières années du XX° Parmi toutes les tentatives de réponses, celle qui va devenir majoritaire est celle de l’éther. Grâce à Maxwell, la lumière est désormais considérée comme une onde électromagnétique mais dans quel milieu se propage-t-elle ? En effet, toutes les ondes connues se propagent dans un milieu matériel : l’eau pour les vagues, l’air pour le son et, de façon générale, la matière pour les vibrations. Enlevez ce milieu et vous supprimez l’onde. On considère alors que la lumière se propage par rapport à l’éther, celui-là même qu’Aristote avait considéré comme le 5° élément, celui qui constitue tout ce qui se trouve dans le monde supralunaire. Mais ce milieu hypothétique doit avoir de singulières propriétés : il n’a pas de masse, il traverse librement la matière, il est infiniment fluide puisqu’il n’oppose aucune résistance au mouvement des astres, il est parfaitement rigide et parfaitement élastique puisque la lumière se transmet suivant une ligne droite et sans atténuation même à des distances considérables. Mais il résout le problème posé par la constante c : il s’agit de la vitesse de la lumière mesurée par rapport au référentiel du milieu dans lequel elle se propage.

L’expérience de Michelson et Morley

Presque aussitôt, une expérience est envisagée pour vérifier la théorie de l’éther : mesurer la vitesse de la lumière depuis le référentiel terrestre dans la direction de déplacement de la Terre autour du Soleil et dans la direction perpendiculaire ; c’est l’expérience de Michelson et Morley du nom des deux physiciens qui vont construire un interféromètre extrêmement sensible pour mettre en évidence une infime variation de la vitesse de la lumière (la vitesse de la Terre autour du Soleil est de 30 km/s à comparer aux 300 000 km/s de la lumière). Les deux physiciens vont réaliser une série d’expériences de 1881 à 1887 pour finalement se rendre à l’évidence : aucune variation de la vitesse de la lumière n’est décelée ! Il faut donc trouver une autre explication à cette constante c qui correspond à la vitesse de la lumière. Pourtant, la théorie de l’éther va subsister jusque vers 1920.

Les deux postulats d’Einstein

La solution à ce problème va finalement être trouvée par un obscur employé de l’office des brevets de Berne, un certain Albert Einstein. Il va parvenir à reformuler rien de moins que les bases de la physique théorique à partir de deux postulats :

• le premier n’est autre que le principe de relativité galiléenne formulé plus haut ;
• le second, beaucoup plus original, est le suivant : la vitesse de la lumière est indépendante de la vitesse de sa source [5].

Autrement dit, quel que soit le référentiel dans lequel vous vous trouvez (et donc quelle que soit la vitesse de la source de lumière dans votre référentiel), vous mesurerez une vitesse de la lumière toujours égale à c. Ainsi, la vitesse de la lumière peut accéder au statut de constante et être utilisée comme telle dans les équations de Maxwell. En revanche, les conséquences de ces deux postulats sont pour le moins étranges et vont clairement à l’encontre du sens commun. C’est d’ailleurs tout le génie d’Einstein (et vraisemblablement de sa première épouse Mileva) que d’avoir continué à explorer une piste qui pouvait sembler aussi déroutante ! La conséquence qui nous intéresse ici et qui n’est pas des moindres par le changement fondamental qu’elle impose dans notre représentation du monde, s’appelle la dilatation des temps.

Ein gedanken Experiment

Reprenons l’expérience par la pensée (gedanken Experiment) d’Einstein [5] : on considère un train qui se déplace suivant un mouvement rectiligne uniforme par rapport au quai de la gare. Dans ce train, on réalise une expérience de physique qui consiste à mesurer le temps que met un faisceau lumineux pour parcourir un aller et retour vertical en se réfléchissant sur un miroir situé à une hauteur H au-dessus de la source de lumière. Sachant que la vitesse de la lumière est c (2e postulat), on en déduit que cette durée d’un aller et retour sera :

Δt=2H/c.

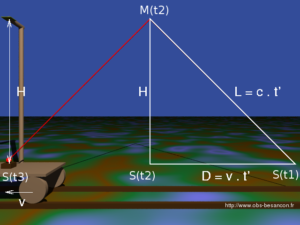
Imaginons maintenant que l’on observe l’expérience depuis le quai de la gare. Dans ce référentiel, le faisceau lumineux part du point A, se réfléchit au point M et arrive finalement au point B. Cette distance AM+MB parcourue par la lumière est incontestablement plus longue que l’aller et retour précédent 2H. Or la vitesse de la lumière est toujours c dans ce référentiel (2° postulat). Par conséquent, la lumière doit parcourir une distance plus longue à la même vitesse : l’expérience dure donc plus longtemps dans le référentiel du quai de la gare que dans le référentiel du train ! Il suffit d’appliquer le théorème de Pythagore pour démontrer que la durée de l’expérience dans ce référentiel vaut :

Δt’=Δt/√1-v²/c².

Bien sûr, la vitesse du train est des millions de fois plus faible que la vitesse de la lumière ce qui rend cet effet insensible. Mais pour autant il existe et on a pu le mesurer avec des horloges atomiques dont une reste au sol tandis que l’autre voyage en avion. La conclusion qui ressort donc de la théorie de la relativité, conclusion amplement vérifiée expérimentalement aujourd’hui, est que les durées, autrement dit l’écoulement du temps, de même d’ailleurs que les distances, autrement dit l’écart entre deux points de l’espace, dépendent du référentiel dans lequel on les mesure. C’en est fini de l’espace et du temps considérés comme cadre indépendant et universel dans lequel évolue le monde : l’espace et le temps sont liés et chaque référentiel induit son propre espace-temps. Einstein ira encore plus loin avec la relativité générale puisqu’il montrera que l’espace-temps est indissociable de la matière qui constitue l’Univers : il n’y a plus un contenant indépendant de son contenu mais un contenant en interaction totale avec son contenu, voire, pour la vision la plus radicale, un contenu sans contenant [6] !

F. Vernotte, 18 mai 2021

[1] BRUNO (Giordano). Le banquet des cendres. – Paris : Ed. de l’Éclat, 2006. 1re éd. : 1584.

[2] GALILEI (Galileo). Dialogue concernant les deux plus grands systèmes du monde. – Paris : Seuil, 2000. (Point Sciences). 1re éd. : 1632.

[3] MAXWELL (James Clerk). A Dynamical Theory of the Electromagnetic Field. Royal Society Transactions, vol. 155, 1865.

[4] HEAVISIDE (Oliver). On the Forces, Stresses and Fluxes of Energy in the Electromagnetic Field. Philosophical Transactions of the Royal Society, vol. 183A, 1892.

[5] EINSTEIN (Albert). La théorie de la relativité restreinte et généralisée (mise à la portée de tout le monde). Paris : Gauthier-Villars, 1921.

[6] ROVELLI (Carlo). Et si le temps n’existait pas. – Paris : Dunod, 2014. (Quai des Sciences). 1re éd. : 2006.